Genetic Algorithm Basics#
Genetic Algorithm Implementation#
Solve a 10-bit binary string optimization problem, in which you need to find the binary string with the largest total bit value.
Population#
import numpy as np
# Set a seed so that the results are consistent over sessions
np.random.seed(3)
def create_binary_population(pop_size, bit_length):
'''
Arguments:
pop_size -- number of individuals inside population
bit_length -- the number of bits of each individual (e.g. [[1010], [1101]])
Return:
binary_pop -- population array of shape (pop_size, bit_length)
'''
binary_pop = np.random.randint(2, size=(pop_size, bit_length))
return binary_pop
pop_size, bit_length = 20, 10
binary_population = create_binary_population(pop_size, bit_length)
population_size = len(binary_population)
print("Population:\n", binary_population)
Fitness#
def fitness_binary_individual(individual):
'''
Return:
fitness -- fitness values, based on number of 1s bits (e.g. [1001] -> 2)
'''
return np.sum(individual)
fitness = np.apply_along_axis(fitness_binary_individual, 1, binary_population)
fitness.shape
print(f'Population:\n{binary_population}\nFitness:\n{fitness}')
Selection#
Use Roulette Wheel Selection to select parents based on their fitness. The probability of selecting an individual is proportional to its fitness.
def rouletter_wheel_selection(population, fitness):
'''
Return:
selected_population -- selected individuals based on fitness
'''
# fitness = fitness.ravel()
fitness_sum = np.sum(fitness)
if fitness_sum == 0:
raise ValueError("Total fitness is zero, cannot perform selection.")
probabilities = fitness / fitness_sum
selected_indices = np.random.choice(len(population), size=len(population), p=probabilities)
selected_population = population[selected_indices]
return selected_population
selected_population = rouletter_wheel_selection(binary_population, fitness)
print(f'Population:\n{binary_population}\nFitness:\n{fitness}\nSelected Population:\n{selected_population}')
Crossover#
def one_point_crossover(parent1, parent2):
'''
Perform one-point crossover between two parents.
Arguments:
parent1 -- first parent binary array
parent2 -- second parent binary array
Return:
child1 -- first child binary array
child2 -- second child binary array
'''
point = np.random.randint(1, len(parent1)) # random integer from low(inclusive) to high(exclusive)
child1 = np.concatenate((parent1[:point], parent2[point:]))
child2 = np.concatenate((parent2[:point], parent1[point:]))
return child1, child2
parent_idx = np.array(np.random.choice(population_size, 2, replace=False))
parent1, parent2 = selected_population[parent_idx]
child1, child2 = one_point_crossover(parent1, parent2)
print(f'Parent 1: {parent1}\nParent 2: {parent2}\nChild 1: {child1}\nChild 2: {child2}')
Mutation#
def bit_flip_mutation(individual, mutation_rate):
random_probs = np.random.random(individual.shape)
return np.where(random_probs < mutation_rate, 1-individual, individual)
mutation_rate = 0.9
# child 1 mutation
child1_mutation = bit_flip_mutation(child1, mutation_rate)
# print(f'Random Probs used to mutate child: {random_probs}')
print(f'Child1: {child1}\nChild1 Mutation: {child1_mutation}')
Replacement and Termination#
import numpy as np
# Set a seed so that the results are consistent over sessions
np.random.seed(3)
def create_binary_population(pop_size, bit_length):
'''
Arguments:
pop_size -- number of individuals inside population
bit_length -- the number of bits of each individual (e.g. [[1010], [1101]])
Return:
binary_pop -- population array of shape (pop_size, bit_length)
'''
binary_pop = np.random.randint(2, size=(pop_size, bit_length))
return binary_pop
def fitness_binary_individual(individual):
'''
Return:
fitness -- fitness values, based on number of 1s bits (e.g. [1001] -> 2)
'''
return np.sum(individual)
def rouletter_wheel_selection(population, fitness):
'''
Return:
selected_population -- selected individuals based on fitness
'''
# fitness = fitness.ravel()
fitness_sum = np.sum(fitness)
if fitness_sum == 0:
raise ValueError("Total fitness is zero, cannot perform selection.")
probabilities = fitness / fitness_sum
selected_indices = np.random.choice(len(population), size=len(population), p=probabilities)
selected_population = population[selected_indices]
return selected_population
def one_point_crossover(parent1, parent2):
'''
Perform one-point crossover between two parents.
Arguments:
parent1 -- first parent binary array
parent2 -- second parent binary array
Return:
child1 -- first child binary array
child2 -- second child binary array
'''
point = np.random.randint(1, len(parent1)) # random integer from low(inclusive) to high(exclusive)
child1 = np.concatenate((parent1[:point], parent2[point:]))
child2 = np.concatenate((parent2[:point], parent1[point:]))
return child1, child2
def bit_flip_mutation(individual, mutation_rate):
random_probs = np.random.random(individual.shape)
return np.where(random_probs < mutation_rate, 1-individual, individual)
population_size = 20
bit_length = 20
n_generations = 70
mutation_rate = 0.01
fitnesses = []
population = create_binary_population(population_size, bit_length)
for i in range(n_generations):
fitness_values = np.apply_along_axis(fitness_binary_individual, 1, population)
fitnesses.append(np.max(fitness_values))
print(f'Best: {fitnesses[-1]}')
selected_population = rouletter_wheel_selection(population, fitness_values)
new_population = []
while(len(new_population) < population_size):
# Selection
# Randomly choose 2 individuals from selected population
parent_idx = np.array(np.random.choice(population_size, 2, replace=False))
parent1, parent2 = selected_population[parent_idx]
# Crossover
child1, child2 = one_point_crossover(parent1, parent2)
# Mutation
child1_mutation = bit_flip_mutation(child1, mutation_rate)
child2_mutation = bit_flip_mutation(child2, mutation_rate)
# Add children to new population
new_population.append(child1_mutation)
new_population.append(child2_mutation)
population = np.array(new_population[:population_size])
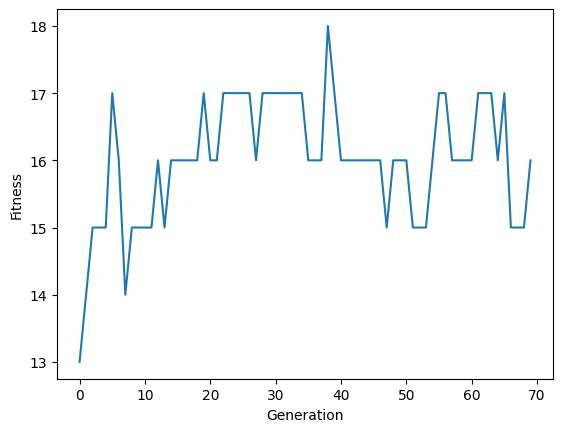
import matplotlib.pyplot as plt
plt.plot(fitnesses)
plt.xlabel('Generation')
plt.ylabel('Fitness');